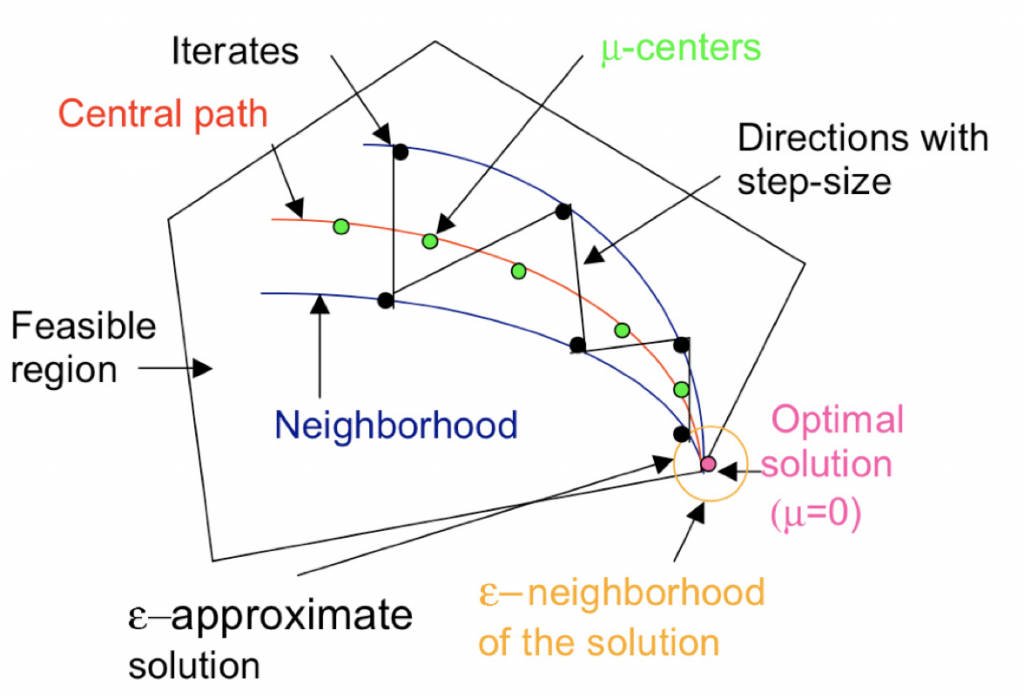
Quantum Interior Point Methods
Making use of Quantum Linear Solvers and Block Encodings to achieve a quantum speedup over classical runtimes by solving the Newton system more efficiently.
Noise in NISQ Devices
Building up a description of physical errors in quantum computers from both individual gate and integrated quantum circuit aspects.
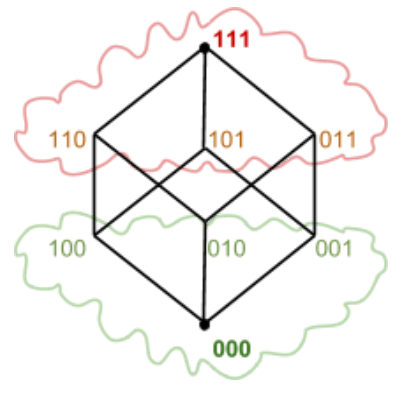
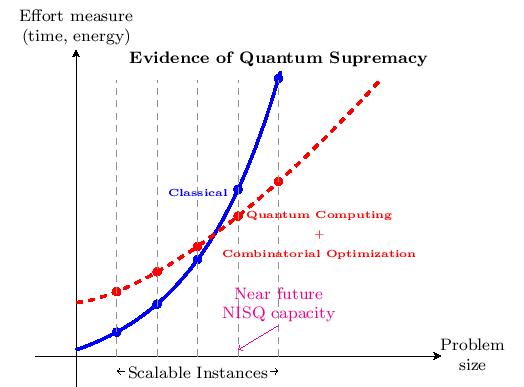
Solving Combinatorial Problems in NISQ devices
Development and study of implementable QUBO formulations of combinatorial problems using QAOA algorithms.
Publications and Reports
- Zheng, M., Li, A., Terlaky, T., & Yang, X. (2020). A bayesian approach for characterizing and mitigating gate and measurement errors. Link: https://arxiv.org/abs/2010.09188
- Pirhooshyaran, M., & Terlaky, T. (2020). Quantum Circuit Design Search. Link: https://arxiv.org/pdf/2012.04046.pdf
- Quintero, R., Bernal, D., Terlaky, T., & Zuluaga, L. F. (2021). Characterization of QUBO reformulations for the maximum k-colorable subgraph problem. Link: https://arxiv.org/abs/2101.09462
- Augustino, B., Nannicini, G., Terlaky, T., & Zuluaga, L. F. (2021). A Quantum Interior Point Method for Semidefinite Optimization Problems. Link: https://engineering.lehigh.edu/sites/engineering.lehigh.edu/files/_DEPARTMENTS/ise/pdf/tech-papers/20/20T_018.pdf
- Mohammdisiahroudi, M., Fakhimi, R., & Terlaky, T. (2021). Efficient Use of Quantum Linear System Algorithms in Interior Point Methods for Linear Optimization. Link: https://engineering.lehigh.edu/sites/engineering.lehigh.edu/files/_DEPARTMENTS/ise/pdf/tech-papers/21/21T_005.pdf
- Mohammdisiahroudi, M., Fakhimi, R., & Terlaky, T. (2021). An Inexact Feasible Interior Point Method for Linear Optimization with High Adaptability to Quantum Computers. Link: https://engineering.lehigh.edu/sites/engineering.lehigh.edu/files/_DEPARTMENTS/ise/pdf/tech-papers/21/21T_006.pdf
- Fakhimi, R., Validi, H., Hicks, I. V., Terlaky, T., & Zuluaga, L. F. (2021). Quantum-inspired formulations for the max 𝑘-cut problem. Link: https://engineering.lehigh.edu/sites/engineering.lehigh.edu/files/_DEPARTMENTS/ise/pdf/tech-papers/21/21T_007.pdf
- Augustino, B., Nannicini, G., Terlaky, T., & Zuluaga, L. F. (2021). An Inexact-Feasible Quantum Interior Point Method for Semidefinite Optimization. Link: https://engineering.lehigh.edu/sites/engineering.lehigh.edu/files/_DEPARTMENTS/ise/pdf/tech-papers/21/21T_008.pdf
- Augustino, B., Nannicini, G., Terlaky, T., & Zuluaga, L. F. (2021). An Inexact-Feasible Quantum Interior Point Method for Second-order Cone Optimization. Link: https://engineering.lehigh.edu/sites/engineering.lehigh.edu/files/_DEPARTMENTS/ise/pdf/tech-papers/21/21T_009.pdf
- Augustino, B., Nannicini, G., Terlaky, T., & Zuluaga, L. F. (2021). An Infeasible-Inexact Quantum Interior Point Method for Convex Quadratic Symmetric Cone Optimization. Link: https://engineering.lehigh.edu/sites/engineering.lehigh.edu/files/_DEPARTMENTS/ise/pdf/tech-papers/21/21T_010.pdf